Every time we publish a drawing or picture of the Copenhagen Suborbitals capsule, someone inevitably asks — sometimes kindly, sometimes anxiously, and sometimes with the same wary tone used by people recalling a long‑haul Ryanair flight:
“Does the astronaut really have to sit like that?”
And honestly?
We couldn’t agree more.
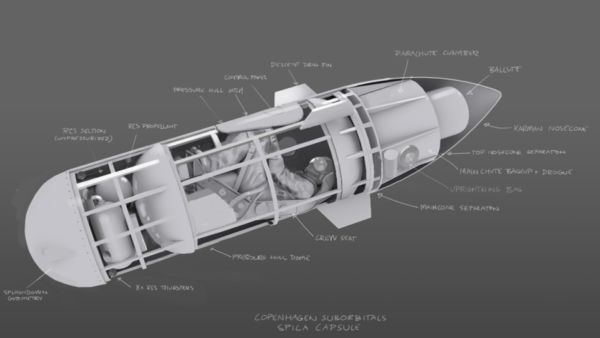
If we had the option, we would love to give the astronaut an extra 10 centimetres of knee room.
We’d love to offer a bit more shoulder space, or a deeper recline, or perhaps even the luxury of not resembling an enthusiastic contortionist.
If comfort alone decided the capsule layout, it would look more like a first‑class sleeper pod than something with the interior optimism of a Ryanair seat.
But physics has no loyalty to comfort.
It doesn’t care about knees, backs, personal space, circulation, ergonomics, or whether the astronaut will want to walk again afterwards.

Physics cares about diameter.
And diameter decides everything.
Gravity Never Takes a Break
Before we dive deeper into drag, diameter, and all the numbers that follow, there’s a fundamental point worth keeping in mind: gravity is always there, pulling against us. Our engines may produce 125 kN of thrust, but with a 5,000‑kilogram rocket, roughly 49 kN of that is immediately consumed just to oppose gravity. Only the remainder is available to accelerate the rocket upwards and push through the atmosphere. And although the rocket becomes lighter as propellant burns, gravity’s influence never disappears — it simply shrinks slightly, but never enough to give us “free thrust”. So every drag value, every performance margin, every diameter comparison in this article is always measured on top of the unavoidable cost of lifting the rocket itself. Gravity is the first enemy we fight, and we fight it all the way up.
The tyranny of diameter
Besides gravity, the rocket engines battles wind resistance also known as drag. Rocket drag depends on a simple equation:
D = ½ × ρ × Cd × A × v²
Two of those terms matter most:
A (frontal area, which depends on diameter²)
v² (velocity squared)
Which means:
• +10% diameter → +21% drag
• +25% diameter → +56% drag
• ×2 diameter → ×4 drag
These are not small penalties.
A slightly wider rocket becomes a radically different rocket — slower, heavier, harder to launch, requiring far more thrust than we have.

So before we choose seating angles, legroom, ergonomics, vibration damping, or splashes of comfort, we must first answer one unforgiving question:
What is the largest diameter we can get away with and still reach space?
For us, that magic number is 1.0 metre.
The reality of building a rocket as volunteers
Our constraints are not theoretical — they are very real*:
• Mass: 5,000 kg
• Engines: 5 × 25 kN = 125 kN total
• Burn time: ~60 seconds
• Target: 105 km
• Budget: easily overshadowed by a medium‑sized office coffee budget
Some years ago, we calculated that our entire annual budget was less than 10% of what NASA spends on coffee.
Not their launch coffee.
Just the coffee.

It was a sobering moment — followed almost immediately by laughter and more coffee.
But it also reinforced something important:
We don’t get to buy our way out of problems.
We solve them with ingenuity, sweat, stubbornness, and the kindness of people who believe in an improbable dream.
A fresh simulation: What happens between 2–10 km
If we make a simple model of the ascent of our 1.0 m diameter rocket and extract its velocity at key altitudes:
| Altitude | Velocity |
| 2 km | ~233 m/s |
| 4 km | ~304 m/s |
| 6 km | ~333 m/s |
| 8 km | ~329 m/s |
| 10 km | ~299 m/s |
The region between 6–10 km is the true battleground.
It’s where drag peaks, where rockets struggle, and where slight design flaws become mission‑ending.
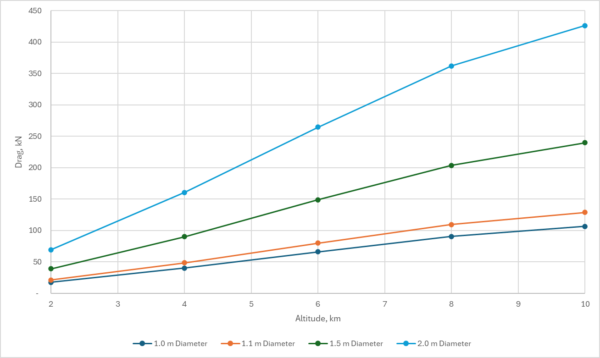
Next, we can calculate the drag at all these altitudes for various capsule diameters:
• 1.0 m
• 1.1 m
• 1.5 m
• 2.0 m
| Altitude \ Diameter of capsule | 1.0 m | 1.1 m | 1.5 m | 2.0 m |
|---|---|---|---|---|
| 2 km | 17.3 kN | 21.0 kN | 39.1 kN | 69.5 kN |
| 4 km | 40.1 kN | 48.6 kN | 90.3 kN | 160.5 kN |
| 6 km | 66.2 kN | 80.1 kN | 148.9 kN | 264.7 kN |
| 8 km | 90.6 kN | 109.6 kN | 203.8 kN | 362.3 kN |
| 10 km | 106,6 kN | 128.9 kN | 239.8 kN | 426.4 kN |
Remember that our total engine thrust available is ~125 kN.
Now compare:
• At 8 km, a 1.5 m diameter rocket already exceeds engine thrust
• At 10 km, a 2.0 m rocket is impossible
• Even 1.1 m eats a painful amount of performance
• Only 1.0 m gets through the drag wall reliably
And this is why the capsule cannot be larger.
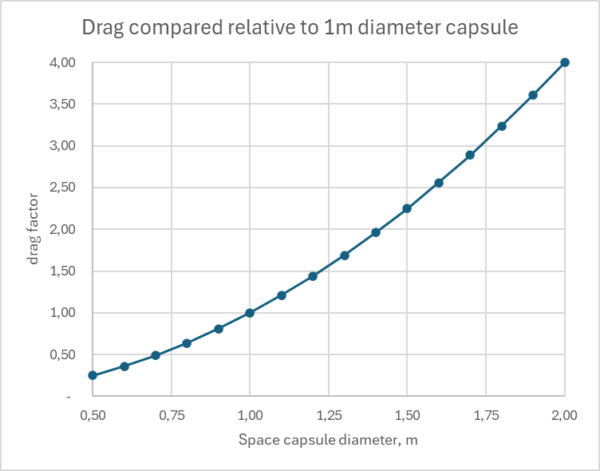
The graph shows exactly what the tables show:
drag rises catastrophically with diameter at the altitudes that matter.

What if we insisted on a 1.25 m capsule?
People sometimes ask:
“Surely 25 centimetres extra can’t hurt?”
Let’s find out.
Drag Increase: +56%
1.25 / 1.0 = 1.25
1.25² = 1.56
So drag increases by 56% everywhere.
At 10 km:
• 1.0 m: 107 kN
• 1.25 m: 167 kN
But the engines can only give us 125 kN.

So what happens?
The rocket slows down.
It cannot climb.
It cannot reach space.
Required thrust: +70%
To maintain performance:
Engine thrust must rise to ≈ 216 kN.
That means either:
• 9 engines instead of 5, or
• 5 engines upgraded to ~43 kN each
With that upgrade, we would need more fuel. MUCH more:
Fuel requirement: +70%
More thrust → more massflow → more propellant.
Propellant must increase from:
• ~3.3 tonnes → ~5.6 tonnes
• Total rocket mass becomes ~7.3 tonnes
• A heavier rocket → even more thrust → even more fuel → even more diameter…
It becomes a spiralling loop of increasing mass and decreasing performance.
This is why:
A 1.25 m capsule is not only difficult – It is impossible for our architecture.
What we can control: The human experience
Although we cannot change the diameter, we can and do improve everything inside the space capsule:
• A carefully optimised semi‑reclined posture
• A spring‑and‑damping system under the seat
• Vibration‑reducing mounts
• A parachute sequence that angles the capsule for a smooth “carving” splashdown
• Drop‑tests with our crash‑test dummy (and eventually, one of us)
• Medical review by a doctor with medical Space experiment experience

It may not be spacious,
but it will be safe and survivable.
The human story behind the numbers
The capsule looks small, but the project behind it is enormous.
Every weld, valve, hinge, bracket, and tank has passed through the hands of volunteers:
People who come to the workshop after work.
People who give up weekends to machine a part, mix fuel, file aluminium, or test parachutes.
People who believe spaceflight should not be reserved for governments and billionaires.
One day, one of us — a volunteer, a friend — will sit inside that capsule.
That reality is why we care obsessively about posture, damping, splashdowns, and safety.
Space is not theoretical when someone you know is inside the rocket.
The paradox we love
The smaller the capsule became,
the bigger the dream grew.
Because the capsule is more than a pressure vessel.
It is a symbol:
That ordinary people can build a spaceship.
That volunteers can reach space.
That a community can accomplish what few thought possible.
When the rocket finally rises above the Baltic Sea,
nobody will be thinking about legroom.
Or posture.
Or Ryanair analogies.

We’ll be thinking about the people who built it —
and the dream this little capsule is carrying into the sky.
It may be the smallest human‑rated capsule in the world.
But it contains one of the biggest dreams humanity has ever had.
*: these are rough values for a simple example, and not the present mission-exact numbers.




